Zertarako erabiltzen dira engranaje epiziklikoak?

Engranaje epiziklikoakEngranaje planetarioen sistemak bezala ere ezagunak, hainbat industriatan erabiltzen dira, diseinu trinkoa, eraginkortasun handia eta moldakortasuna direla eta.

Engranaje hauek batez ere espazio mugatua dagoen aplikazioetan erabiltzen dira, baina momentu eta abiadura aldakortasun handia ezinbestekoak direnean.

1. Automobilen transmisioak: Engranaje epiziklikoak funtsezko osagaiak dira transmisio automatikoetan, martxa-aldaketa ezin hobeak, momentu handia abiadura baxuetan eta potentzia-transferentzia eraginkorra eskaintzen baitituzte.
2. Industria-makineria: Makineria astunetan erabiltzen dira karga handiak maneiatzeko, momentua modu uniformean banatzeko eta espazio trinkoetan eraginkortasunez funtzionatzeko duten gaitasunagatik.
3. Aire eta espazioa: Engranaje hauek funtsezko zeregina dute hegazkinen motorretan eta helikopteroen errotoreetan, fidagarritasuna eta mugimenduaren kontrol zehatza bermatuz baldintza zorrotzetan.
4. Robotika eta automatizazioa: Robotikan, engranaje epiziklikoak erabiltzen dira mugimendu-kontrol zehatza, diseinu trinkoa eta momentu handia lortzeko espazio mugatuetan.

Zeintzuk dira engranaje epizikliko multzoaren lau elementuak?

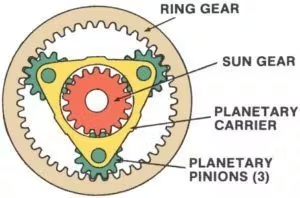
Engranaje epizikliko multzoa, izenez ere ezagutzen denaplaneta-engranajea sistema, oso mekanismo eraginkor eta trinkoa da, automobilen transmisioetan, robotikan eta industria-makinetan erabili ohi dena. Sistema hau lau elementu nagusiz osatuta dago:

1.Eguzki-ekipoaEngranaje multzoaren erdian kokatuta, eguzki-engranajea mugimenduaren eragile edo hartzaile nagusia da. Planeta-engranajeekin zuzenean lotzen da eta askotan sistemaren sarrera edo irteera gisa balio du.

2. Planeta-engranajeakEguzki-engranajearen inguruan biratzen diren hainbat engranaje dira. Planeta-euskarri batean muntatuta, eguzki-engranajearekin eta eraztun-engranajearekin engranatzen dira. Planeta-engranajeek karga uniformeki banatzen dute, sistemak momentu handia kudeatzeko gai bihurtuz.

3.Planeta-garraiatzaileaOsagai honek planeta-engranajeak bere lekuan eusten ditu eta eguzki-engranajearen inguruan biratzea ahalbidetzen du. Planeta-euskarriak sarrera, irteera edo elementu geldikor gisa joka dezake sistemaren konfigurazioaren arabera.

4.Eraztun-engranajeaPlaneta-engranajeak inguratzen dituen kanpoko engranaje handi bat da. Eraztun-engranajearen barneko hortzak planeta-engranajeekin bat egiten dute. Beste elementuak bezala, eraztun-engranajea sarrera, irteera edo geldirik egon daiteke.

Lau elementu hauen elkarrekintzak malgutasuna ematen du abiadura-erlazio eta norabide-aldaketa desberdinak lortzeko egitura trinkoa batean.

Nola kalkulatu engranaje-erlazioa engranaje epizikliko multzo batean?

Engranaje-erlazioaengranaje epizikliko multzoa zein osagai diren finkoak, sarrerakoak eta irteerakoak araberakoa da. Hona hemen engranaje-erlazioa kalkulatzeko urratsez urratseko gida:

1. Ulertu sistemaren konfigurazioa:

Zehaztu zein elementu (eguzkia, planeta-eramailea edo eraztuna) dagoen geldirik.

Zehaztu sarrera eta irteera osagaiak.

2. Erabili oinarrizko engranaje-erlazioaren ekuazioa: Engranaje epizikliko baten engranaje-erlazioa honela kalkula daiteke:

GR = 1 + (R / S)

Non:

GR = Engranaje-erlazioa

R = Engranaje eraztunaren hortz kopurua

S = Eguzki-engranajearen hortz kopurua

Ekuazio hau aplikatzen da planeta-eramailea irteera denean, eta eguzkia edo eraztun-engranajea geldirik dagoenean.

3. Beste konfigurazio batzuetarako egokitu:

• Eguzki-engranajea geldirik badago, sistemaren irteerako abiadura eraztun-engranajearen eta planeta-eramailearen arteko erlazioak eragiten du.
• Eraztun-engranajea geldirik badago, irteerako abiadura eguzki-engranajearen eta planeta-eramailearen arteko erlazioak zehazten du.

4. Alderantzizko engranaje-erlazioa irteeratik sarrerara: Abiadura-murrizketa kalkulatzerakoan (sarrera irteera baino handiagoa), erlazioa erraza da. Abiadura-biderkadura egiteko (irteera sarrera baino handiagoa), kalkulatutako erlazioa alderantzikatu.

Kalkuluaren adibidea:

Demagun engranaje multzo batek honako hau duela:

Eraztun-engranajea (R): 72 hortz

Eguzki-engranajea (S): 24 hortz

Planeta-eramailea irteera bada eta eguzki-engranajea geldirik badago, engranaje-erlazioa hau da:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

Horrek esan nahi du irteerako abiadura sarrerako abiadura baino 4 aldiz motelagoa izango dela, 4:1eko murrizketa-erlazioa emanez.

Printzipio hauek ulertzeak ingeniariei aplikazio espezifikoetara egokitutako sistema eraginkorrak eta moldagarriak diseinatzeko aukera ematen die.